Braids from Lorenz orbits

The Lorenz system

The Lorenz system is a system of differential equations given by

\begin{align} & \frac{\mathrm{d} x}{\mathrm{~d} t}=\sigma(y-x) \cr & \frac{\mathrm{d} y}{\mathrm{~d} t}=x(\rho-z)-y \cr & \frac{\mathrm{d} z}{\mathrm{~d} t}=x y-\beta z \end{align}

The original parameters studied by Lorenz were $\rho=28, \sigma=10, \beta=8/3$ . For those parameters, the system exhibits a well-known “Butterfly-like attractor” with two lobes:

Among all orbits of the system, some of them form closed loops. They can be visually described by recording the sequence of lobes visited (R for right, L for left). This is best visualized through a template:

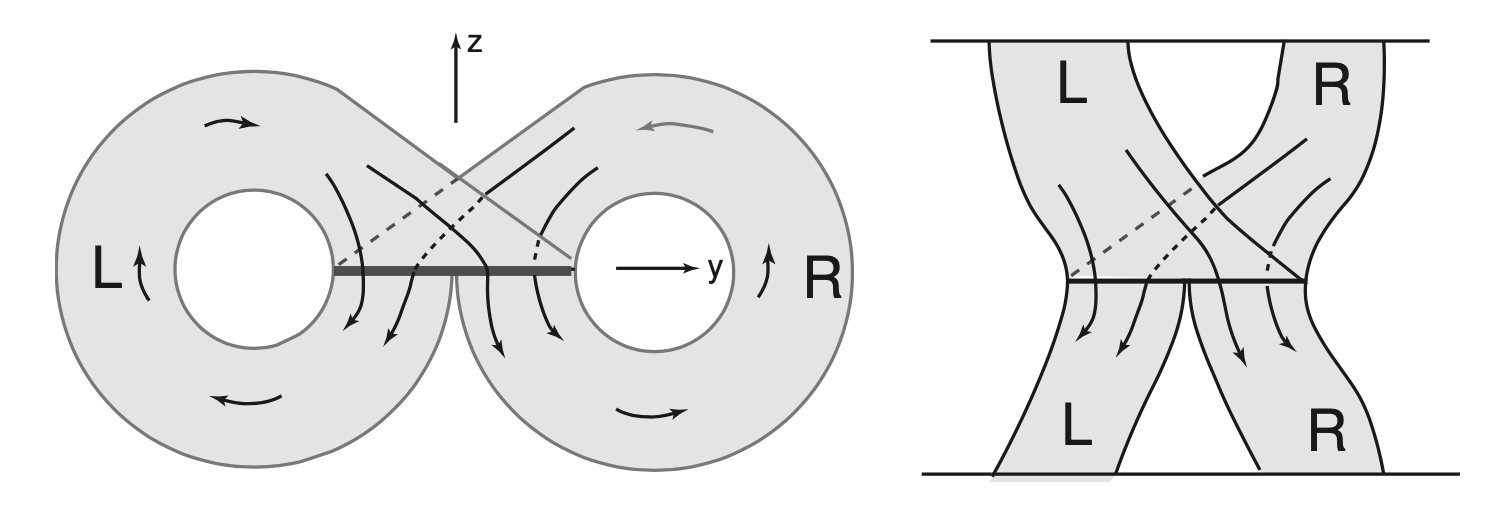
Closed braids as words

I wrote he small library LorenzBraids to be able to convert automatically a closed orbit given as a word, say LRLRRRLRRR, into a braid word (see Braid group) recording the crossings of the strands. The library also computes the braid in its ‘Dowker code’ form (Dowker notation).

The usage is very simple:

knot_string = 'LRLRRRLRRR'
lk = LorenzKnot(knot_string)
knot_code = str(lk.dowker_code())
print(f'The Lorenz Knot with word {knot_string} has Dowker code {knot_code}\n')
lk.convert_to_braid()
print(lk.braid)
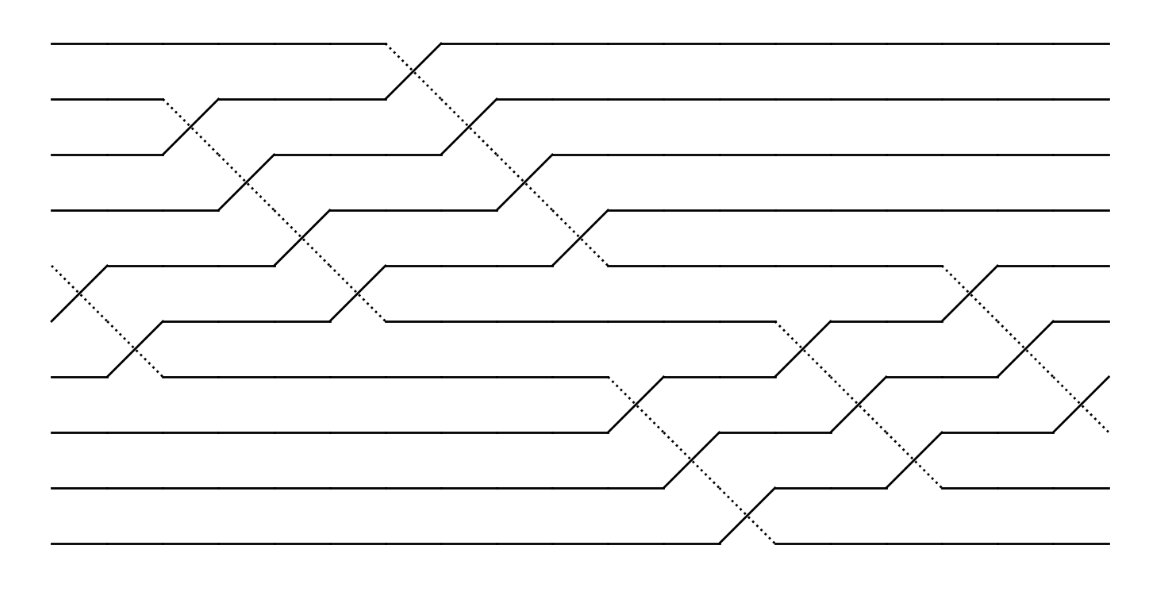
>>> [4, 3, 7, 6, 5, 4, 8, 7, 6, 5, 2, 1, 0, 3, 2, 1, 4, 3, 2]

The braid with its simple description can now be visualized :

braid_word = [4, 3, 7, 6, 5, 4, 8, 7, 6, 5, 2, 1, 0, 3, 2, 1, 4, 3, 2]
plot_braid(braid_word)

Hyperbolic volumes

One of the reasons why I wrote these scripts was to be able to feed directly a closed orbit into Snappy to be able to check when the (closed) orbit complement is hyperbolic. Snappy does the computation of the hyperbolic volume for such braids immediately:

import snappy as sn
from snappy import manifolds
from spherogram.codecs import DT

M = sn.Manifold('Braid[5, 4, 8, 7, 6, 5, 9, 8, 7, 6, 3, 2, 1, 4, 3, 2, 5, 4, 3]')
M.volume()
>>> 7.70691180281